doi: 10.56294/hl2024.477

ORIGINAL

Application of Benford’s Law in The Results of the 2023 Presidential Elections, Second Round in Ecuador

Aplicación de Ley Benford en Resultados de Elecciones Presidenciales de 2023, Segunda Vuelta en Ecuador

Mayra Alexandra Granda Sanmartín¹ *, Edgar Ernesto Lascano Corrales¹ *, Carlos Iván Lucina Cabezas¹ *, Pedro Homero Janeta Tenelema¹ *

¹Universidad Regional Autónoma de los Andes (UNIANDES). Ecuador.

Citar como: Granda Sanmartin MA, Lascano Corrales EE, Lucina Cabezas CI, Janeta Tenelema PH. Application of benford’s law in the results of the 2023 presidential elections, second round in ecuador. Health Leadership and Quality of Life. 2024; 3:.477. https://doi.org/10.56294/hl2024.477

Enviado: 15-03-2024                   Revisado: 04-08-2024                   Aceptado: 21-11-2024                 Publicado: 22-11-2024

Editor: PhD. Prof. Neela Satheesh

Autor para la correspondencia: Mayra Alexandra Granda Sanmartín *

ABSTRACT

Benford’s Law is a statistical tool used to analyze the distribution of digits in a dataset. This law posits that, in many cases, the first digit of a number is not random but follows a specific distribution, with the digit 1 being the most common, followed by 2, 3, and so on. This article analyzed the application of Benford’s Law, through the distribution of the first digits of numbers across various datasets, to the results of the 2023 presidential elections, second round, in Ecuador. The objective was to detect potential anomalies or manipulations in the vote count. The authors used the official data published by the National Electoral Council of Ecuador and compared it with the expected values according to Benford’s Law. The results showed that most provinces complied with Benford’s Law, with some exceptions that could be attributed to random factors or irregularities. The authors conclude that Benford’s Law is a useful, though not definitive, tool for assessing the integrity of electoral processes.

Keywords: Benford’s Law; Electoral Analysis; Fraud Detection; Presidential Elections; Vote Integrity.

RESUMEN

La ley de Benford es una herramienta estadística que se utiliza para analizar la distribución de los dígitos en un conjunto de datos. Esta ley establece que, en muchos casos, el primer dígito de un número no es aleatorio, sino que sigue una distribución específica, en particular, el dígito 1 es el más común, seguido del 2, el 3, y así sucesivamente. El artículo analizó la aplicación de la ley Benford, mediante la distribución de los primeros dígitos de los números en muchos conjuntos de datos, a los resultados de las elecciones presidenciales de 2023, segunda vuelta, en Ecuador. El objetivo fue detectar posibles anomalías o manipulaciones en el conteo de votos. Los autores utilizaron los datos oficiales publicados por el Consejo Nacional Electoral de Ecuador y los compararon con los valores esperados según la ley Benford. Los resultados mostraron que la mayoría de las provincias cumplen con la ley Benford, salvo algunas excepciones que podrían deberse a factores aleatorios o a irregularidades. Los autores concluyen que la ley Benford es una herramienta útil pero no definitiva para evaluar la integridad de los procesos electorales.

Palabras clave: Ley de Benford; Análisis Electoral; Detección de Fraude; Elecciones Presidenciales; Integridad del Voto.

INTRODUCCIÓN

La historia de la ley de Benford se remonta al siglo XIX, cuando el astrónomo y matemático Simon Newcomb observa que las primeras páginas de las tablas de logaritmos estaban más desgastadas que las últimas. Este descubrimiento lo lleva a deducir que los números cuyo primer dígito es 1 aparecen con más frecuencia que aquellos que comienzan con 9. Específicamente, la distribución de los primeros dígitos del 1 al 9 tiene los siguientes porcentajes de aparición: 1) 30,1 %, 2) 17,6 %, 3) 12,5 %, 4) 9,7 %, 5) 7,9 %, 6) 6,7 %, 7) 5,8 %, 8) 5,1 %, 9) 4,6 %. Sin embargo, Newcomb no presenta una fórmula matemática ni evidencia estadística que respaldara su hallazgo.^(1,2)

La ley de Benford, también conocida como la “ley del primer dígito”, fue retomada por el físico Frank Benford, quien realiza un estudio empírico con más de 20 000 números de diversas fuentes, como áreas fluviales, constantes físicas y direcciones. Benford encuentra que la distribución de los primeros dígitos sigue una ley logarítmica, que hoy en día se conoce como la ley de Benford. Esta ley cobra mayor relevancia en los campos de las matemáticas y la estadística en la década de 1990, cuando es redescubierta por el matemático Theodore Hill.⁽³⁾ Desde entonces, se ha aplicado en numerosos campos, como la contabilidad, las finanzas, la salud y los procesos electorales, para identificar irregularidades o posibles fraudes en los datos numéricos.^(4,5,6)

En el ámbito financiero, varios estudios han utilizado la ley de Benford para detectar fraudes y evaluar la precisión de los informes financieros. Se ha encontrado que desviaciones del patrón esperado en la frecuencia del primer dígito pueden indicar manipulación de datos. Asimismo, se ha empleado para analizar la exactitud de los informes financieros de organizaciones sin fines de lucro y detectar posibles fraudes en los datos aduaneros recopilados en el comercio internacional.^(7,8) Además, se ha aplicado en el análisis de las intervenciones gerenciales en el proceso de asignación de capital.⁽⁹⁾

En el ámbito académico, la ley de Benford ha sido utilizada para evaluar resultados de investigaciones y detectar anomalías. Un estudio en Eslovenia concluye que el número de artículos por investigador sigue la distribución de Benford, mientras que el número de autores por artículo no, lo que lleva a la identificación de algunas anomalías explicables.⁽¹⁰⁾

En el campo de la salud, la ley de Benford se ha aplicado para evaluar los sistemas de vigilancia epidemiológica, especialmente durante epidemias.⁽¹¹⁾ En el ámbito ambiental, se ha utilizado para investigar alteraciones en series hidrológicas temporales, encontrando inconsistencias que podrían sugerir sesgos, errores, modificaciones de los datos o la influencia de factores externos como el cambio climático.⁽¹²⁾

En la era digital, la ley de Benford se ha aplicado en el análisis forense de imágenes para detectar falsificaciones. Singh et al.⁽¹³⁾ descubrieron que las imágenes JPEG y JPEG2000 siguen esta ley, siendo más precisa en el formato JPEG2000. Por su parte, Parnak et al.⁽¹⁴⁾ proponen un algoritmo de detección de falsificaciones basado en variantes de la ley de Benford, logrando una precisión superior a otros métodos. Frick et al.⁽¹⁵⁾ proponen un marco de detección forense pasiva basado en artefactos de compresión y la ley del primer dígito, obteniendo valores altos de AUC en la clasificación de imágenes de alta calidad.

Este estudio se justifica porque el análisis de los procesos electorales es crucial para garantizar la transparencia y la legitimidad de las elecciones, pilares fundamentales de las democracias modernas. La ley de Benford, como herramienta estadística, ha demostrado ser eficaz en la detección de irregularidades numéricas en diversas áreas, incluidas las elecciones. Dada la creciente preocupación sobre posibles manipulaciones en los resultados electorales en diversos contextos, este estudio aplica la ley de Benford a los resultados de la segunda vuelta de las elecciones presidenciales de 2023 en Ecuador, con el objetivo de contribuir a la detección de anomalías que puedan comprometer la integridad del proceso electoral. Esta investigación no solo refuerza los mecanismos de auditoría electoral, sino que también aporta una metodología replicable para estudios futuros en otros países y contextos.

Los autores del presente estudio pretenden responder la pregunta de investigación: ¿Los resultados de la segunda vuelta de las elecciones presidenciales de 2023 en Ecuador cumplen con las expectativas de la ley de Benford?

Por ello, el objetivo de la presente investigación es detectar posibles anomalías o manipulaciones en el conteo de votos en la segunda vuelta de las elecciones presidenciales de la república de Ecuador en 2023, verificando su consistencia con la distribución de primeros dígitos según la ley de Benford, contribuyendo a un proceso electoral justo y transparente.

MÉTODO

Se trata de un estudio cuantitativo con un tipo de investigación transversal y relacional, en el cual incluye la ley estadística-matemática de Benford y la distribución del primer dígito de la totalidad de las bases de datos del proceso elecciones presidenciales 2023, segunda vuelta, de fecha 15 de octubre del 2023.

En relación con los alcances de investigación se utilizaron descriptivo y exploratorio, en el primer caso se caracterizó los resultados en función al número de mesas por provincia y también al nivel de correlación, adicional en la introducción se describieron las diferentes investigaciones que sirvieron como aporte al estudio. En el segundo caso la presente investigación servirá de fuente para futuras investigaciones relacionadas al proceso electoral.

Este estudio se basó en el modelo estadístico matemático conocido como la ley de Benford (1938), que permite comparar las distribuciones de los resultados de las elecciones presidenciales a nivel provincial y nacional con las distribuciones de dicha ley. Así, se calcularon los coeficientes de correlación simple y de r cuadrado ajustado para determinar si se cumplía o no este principio cuantitativo.

En referencia con la determinación de la muestra, se estableció aquellas provincias cuyo número de mesas electorales superen 100 y que, de aquellos resultados provinciales, en cualesquiera de las variables votos presidenciable Daniel Noboa, votos presidenciable Luisa González, votos nulos y votos blanco, el coeficiente de correlación simple sea inferior a 0,70. Entonces una vez recolectada y procesada la información a través de la herramienta Microsoft Excel 365 y con el modelo matemático de Benford, se establece la muestra con las características antes mencionadas.

Se utilizó la técnica de muestreo no probabilístico por conveniencia, debido a que únicamente se presentan dos candidatos a la presidencia, además de votos nulos y votos blancos, cuyos valores no sugieren representatividad estadística, para aquello se aplicó la prueba estadística de Kolmogorov-Smirnov, a fin de establecer si la muestra proviene de una distribución específica. Para esto se determina la hipótesis nula y la hipótesis alternativa.

· Hipótesis nula Ho: los resultados del registro de mesas no se correlacionan significativamente con la ley de Benford.

· Hipótesis alternativa H1: los resultados del registro de mesas se correlacionan significativamente con la Ley de Benford.

Los criterios que determinan la normalidad son: Sig. = > α se acepta H0 = los valores vienen de una distribución normal, en cambio Sig. < α se acepta Hi = los valores no vienen de una distribución normal. Los resultados indican que el resultado del Sig., en todas las provincias de estudio resultaron menores que el rango de significancia α= 0,05, mostrando que las cifras tienen distribución normal con excepción de Los Ríos.

Para la categorización e interpretación del nivel de correlaciones de las muestras de cada provincia y decisión de voto, se optó por aproximaciones como se expone en la tabla 1 la siguiente manera.

Tabla 1. Categorización para la interpretación de nivel de correlaciones

Categorización

0,70 o + Correlación fuerte

Entre 0,70 y - Correlación de análisis

En primera instancia, se puede interpretar que de la información procesada en función a las condiciones de que, por provincia, el número de mesas sea igual o superior a 100, que el índice de correlación a nivel provincial sea inferior 0,70, en cualquiera de las variables. Por lo tanto, se establece que el 46 % de los votantes le dieron la victoria al candidato Noboa, mientras 45 % correspondió a la candidata Gonzales, el 8 % reflejó los votos nulos y el 1 % los votos en blanco.

En la tabla 2 se desglosan los votantes por las provincias ecuatorianas.

Tabla 2. Total de votantes por provincia
No.	Provincia	Blanco	Nulo	Daniel	Luisa	Total
1	Azuay	236	4332	32556	18773	55897
2	Bolívar	191	2455	11858	7872	22376
3	Cañar	299	4013	33730	13678	51720
4	Cotopaxi	134	2801	18928	8717	30580
5	El oro	174	1975	14897	13765	30811
6	Guayas	1017	6929	34970	43716	86632
7	Imbabura	260	2781	11142	12938	27121
8	Loja	190	2002	30234	9340	41766
9	Los rios	449	2496	5913	19010	27868
10	Manabi	1847	13753	60321	111854	187775
11	Pichincha	338	6726	45757	29887	82708
12	Sto dgo tsachilas	337	2954	13408	21182	37881
	Total	5472	53217	313714	310732	683135
	%	1	8	46	45	100

RESULTADOS

Se realizaron análisis individuales por provincias, entre los resultados de los candidatos y la ley de Benford, según cuadro general que se presenta en la tabla 3.

Tabla 3. Correlaciones estadísticas de resultados provinciales con ley de Benford
No.	Provincia	Nulos		Blancos		Noboa		Luisa
		r	r2 Ajustado	r	r2 Ajustado	r	r2 Ajustado	r	r2 Ajustado
1	Azuay	0,80	0,64	0,98	0,97	0,89	0,80	0,40	0,16
2	Bolivar	0,78	0,60	0,90	0,80	0,93	0,87	0,76	0,58
3	Cañar	0,98	0,96	0,99	0,99	0,94	0,88	-0,36	0,13
4	Cotopaxi	0,57	0,33	0,96	0,93	0,96	0,92	-0,15	0,02
5	El oro	0,95	0,90	0,93	0,86	0,86	0,74	0,80	0,74
6	Guayas	0,86	0,74	0,80	0,65	0,78	0,61	0,93	0,86
7	Imbabura	0,72	0,51	0,81	0,66	0,79	0,62	0,89	0,80
8	Loja	0,88	0,77	0,99	0,98	0,57	0,32	-0,37	0,13
9	Los rios	0,57	0,32	0,67	0,45	-0,31	0,09	0,52	0,27
10	Manabi	0,93	0,86	0,97	0,94	0,70	0,48	0,95	0,91
11	Pichincha	0,84	0,71	0,99	0,98	0,87	0,76	0,47	0,23
12	Santo domingo	0,67	0,45	0,67	0,45	0,79	0,63	0,89	0,80
Fuente: Pagina CNE.

Para el caso de la provincia de Azuay (figura 1) se observa que el coeficiente de correlación de resultados de los dos candidatos es disímil, para el caso de Noboa es 0,9 y para Gonzáles es 0,4, con el mismo volumen de datos para esta provincia.

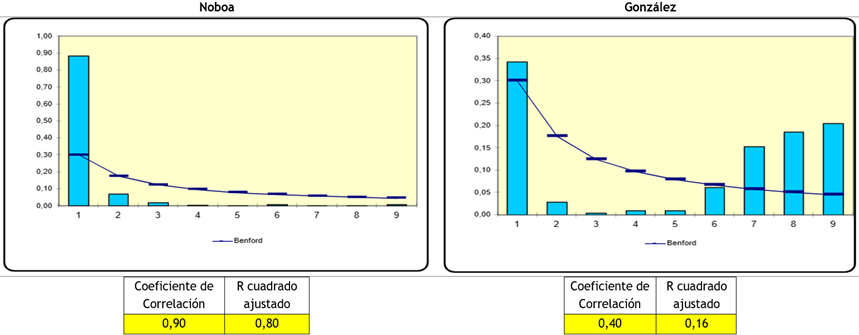
Figura 1. Ley Benford Provincia Azuay

Para Bolívar, al igual que la provincia anterior, se observa una relación, entre sus resultados y la LB, de 0,94 para el caso de Noboa y 0,77 para la candidata González (figura 2).

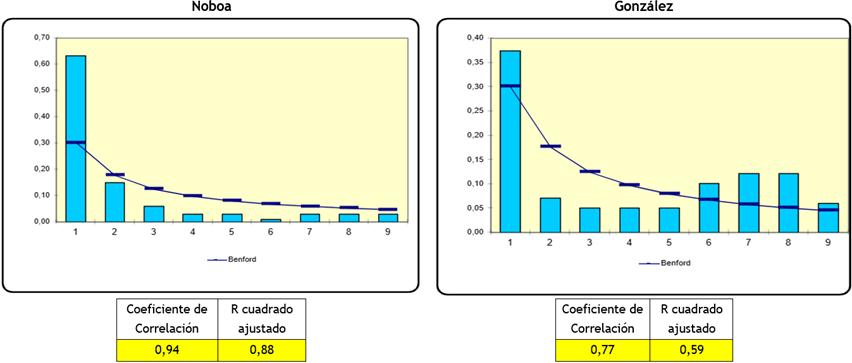
Figura 2. Ley Benford Provincia Bolívar

La provincia de Cañar tiene un comportamiento mucho más extremo que la primera provincia analizada, para el caso del candidato Noboa el coeficiente de correlación de sus resultados con la LB es de 0,94 y para la candidata González la correlación en negativa -0,34 (figura 3).

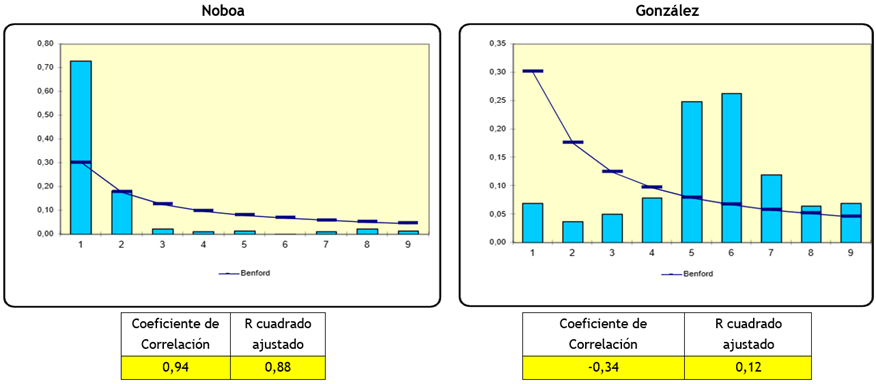
Figura 3. Ley Benford Provincia Cañar

Una tendencia similar a la descrita en la provincia anterior se produce en Cotopaxi, con una alta relación para el candidato Noboa 0,91 y negativa o inversamente proporcional para la candidata González -0,15 (figura 4).

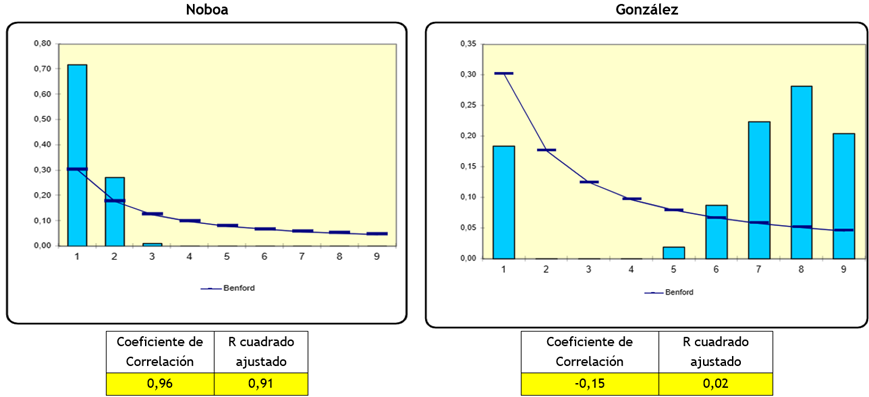
Figura 4. Ley Benford Provincia Cotopaxi

En la provincia de El Oro existe mayor consistencia que las descritas anteriormente, el candidato Noboa obtuvo una correlación de 0,86 y la candidata González de 0,8 (figura 5).

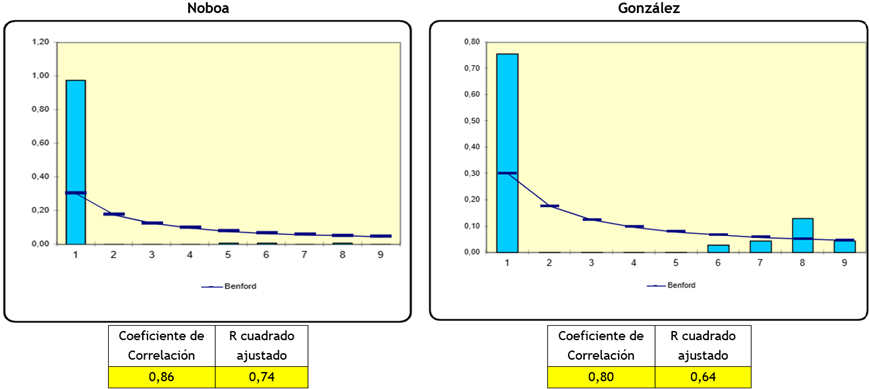
Figura 5. Ley Benford Provincia El Oro

Guayas es la primera del análisis individual por provincia en que la candidata González obtuvo una mayor correlación con 0,93, mientras que para el candidato Noboa fue de 0,78 (figura 6).

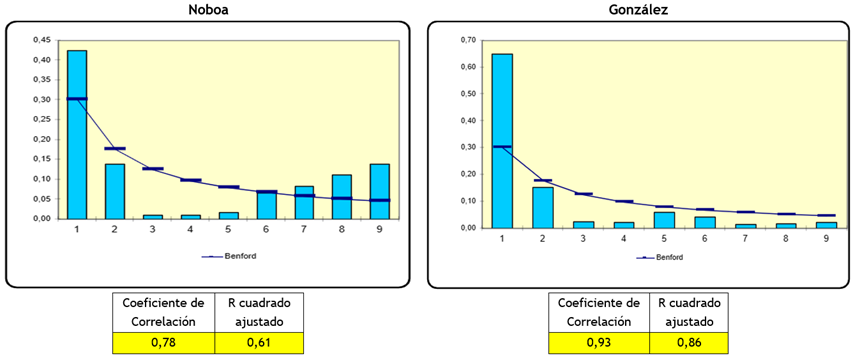
Figura 6. Ley Benford Provincia Guayas

En Imbabura se produce el mismo comportamiento de Guayas, la candidata González obtuvo una mayor correlación comparada con el candidato Noboa, 0,89 y 0,79 respectivamente.

De la misma forma que en la provincia de Cañar y Cotopaxi, el resultado en la provincia de Loja fue una alta relación para el candidato Noboa 0,57 y negativa o inversamente proporcional para la candidata González -0,37 (figura 7).

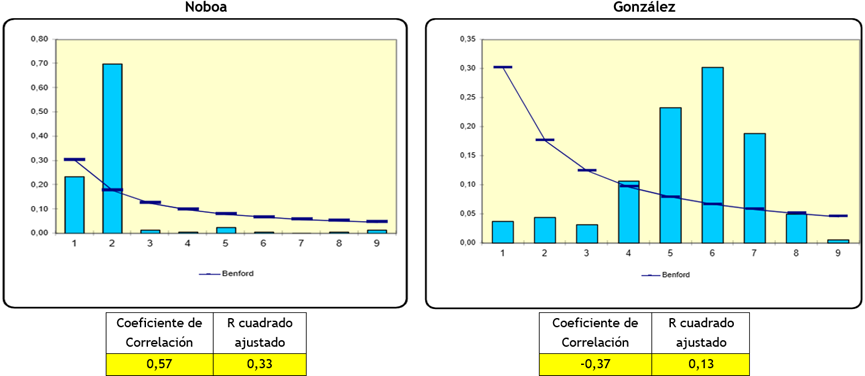
Figura 7. Ley Benford Provincia Loja

En la provincia de Los Ríos se evidencia que el coeficiente de correlación de los resultados en esta provincia fue de negativo para Noboa -0,31 y para González de 0,53 (figura 8).

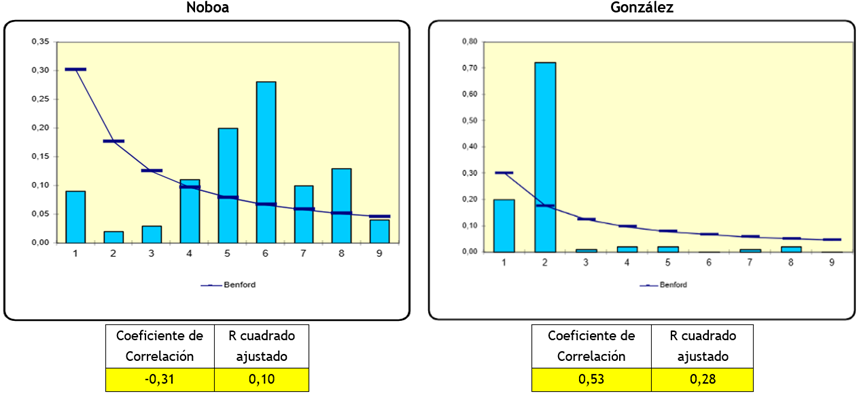
Figura 8. Ley Benford Provincia Los Ríos

Manabí es otra de las provincias en que se evidencia que la candidata González tiene una correlación más alta 0,95 que el del candidato Noboa 0,69.

En la provincia de Pichincha el candidato Noboa obtiene una correlación de 0,87 mientras que su contrincante, González, obtuvo 0,48. Finalmente, se observa que en la relación de resultados con la ley de Benford de los dos candidatos, Noboa y González, en Provincia Santo Domingo de los Tsáchilas los resultados de las correlaciones son 0,79 y 0,89 respectivamente.

A nivel nacional se puede evidenciar que de acuerdo con el modelo de Benford, se cumple con una correlación alta, en el caso de del candidato Noboa la correlación fue de 88, Gonzales 87, votos nulos 91, votos blancos 97. Sin embargo, esta interpretación habría que matizarla dado que, al tratarse de una gran cantidad de mesas y votos, obtener una relación de menos de 0,90 es suficiente razón para realizar análisis más detallados por provincia que a continuación se presenta en la figura 9.

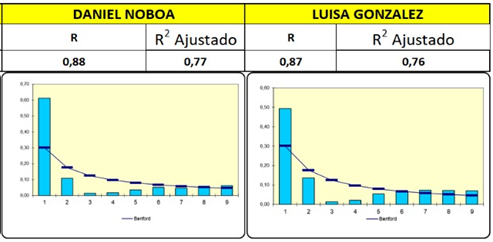
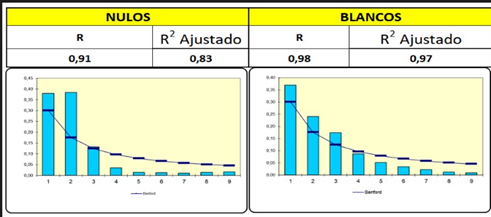
Figura 9. Comparación registro de mesas electorales y Modelo Benford

DISCUSIÓN

En las diversas investigaciones en el campo de contabilidad, finanzas, salud, porcesos electorales, autores como Handoko et al.⁽⁴⁾; Kössler et al.⁽⁵⁾; Morales et al.⁽⁶⁾, Mouaaouy et al.⁽⁹⁾, Tošic et al.⁽¹⁰⁾, Moreno-Montoya⁽¹¹⁾, sugieren la aplicación de la ley benford con el objetivo de identificar irregularidades, manipulaciones de bases de datos o fraude.

De acuerdo con los estudios de Singh et al.⁽¹³⁾, Parnak et al.⁽¹⁴⁾ comprobaron la aplicación de la ley en el campo de analisis forence de imágenes para detectar falsificacion.

En referencia a los autores Lascano et al.⁽¹⁶⁾ y Gueron et al.⁽¹⁷⁾, en sus estudios muestran similitud con los resultados de la presente investigación. En los procesos electorales, existen diversos estudios que han aplicado la ley de Benford para detectar irregularidades. Por ejemplo, en las elecciones para la alcaldía de Quito en 2019, los resultados de los cuatro primeros candidatos no cumplieron con la ley, mientras que los candidatos con menor votación sí lo hicieron.⁽¹⁶⁾

En contraste, las elecciones al Senado brasileño de 1994 muestran conformidad con la ley de Benford.⁽¹⁷⁾ Además, Eichhorn⁽¹⁸⁾ analizó el impacto de la digitalización y el voto electrónico en la manipulación electoral en las elecciones de gobernadores en Rusia, encontrando mayor inconsistencia en los distritos digitales, lo que sugiere que estas tecnologías pueden ser utilizadas para complementar o reemplazar métodos tradicionales de manipulación electoral. Este estudio también cuestiona la afirmación de que la digitalización aumenta la legitimidad, inclusión y transparencia en elecciones de estados autoritarios.

Dada la relevancia del presente análisis basado en la ley de Benford sobre los resultados de las elecciones presidenciales de 2023 en Ecuador, un estudio futuro podría aplicar la neutrosofía para profundizar en la evaluación de posibles irregularidades electorales. La neutrosofía, como marco matemático que trata con el análisis de sistemas complejos en los que intervienen componentes verídicos, falsos y neutros, permitiría incorporar un enfoque más flexible para manejar la incertidumbre y la ambigüedad en los datos electorales. Esto es particularmente relevante en escenarios donde los resultados numéricos pueden verse afectados por factores impredecibles o poco transparentes, que no necesariamente siguen patrones esperados.

La neutrosofía ha mostrado ser exitosa en otros campos investigativos como el análisis de la contratación pública durante la emergencia sanitaria, la evaluación de la pertinencia de la atención médica intercultural y la medición de la satisfacción de usuarios en entornos virtuales de aprendizaje.^(19,20,21) Por lo tanto, su aplicación en el análisis electoral permitiría evaluar con mayor precisión la integridad de los resultados electorales y podría identificar patrones más complejos de manipulación o irregularidades que los métodos tradicionales no detectan.

Este estudio futuro ampliaría la comprensión sobre la fiabilidad de los procesos electorales y proporcionaría nuevas herramientas para fortalecer la transparencia y la confianza en los resultados, en un contexto donde los datos electorales se vuelven cada vez más sofisticados y vulnerables a influencias externas.

CONCLUSIONES

La ley de Benford establece que la distribución de los primeros dígitos de los números que aparecen en fuentes naturales o sociales sigue un patrón predecible, donde los dígitos más bajos son más frecuentes que los más altos.

El artículo aplica esta ley a los resultados de la segunda vuelta de las elecciones presidenciales de 2023 en Ecuador, donde se enfrentaron los candidatos Noboa y Gonzales.

El artículo concluye que los resultados electorales se ajustan a la ley de Benford, lo que sugiere que no hubo manipulación o alteración de los datos agregados, aunque habrá que analizar con mayor profundidad ciertas provincias descritas. Sin embargo, el artículo también reconoce algunas limitaciones de la ley de Benford, como, por ejemplo: que no es una prueba definitiva de fraude o honestidad, que depende de la calidad y el tamaño de la muestra de datos, y que puede haber factores que influyan en la distribución de los dígitos sin implicar irregularidades.

El artículo también destaca las ventajas de la ley de Benford como herramienta para evaluar la integridad de los procesos electorales, como, por ejemplo: que es fácil de aplicar y entender, que es universal y no depende del contexto, y que puede servir como una alerta temprana para investigar posibles anomalías.

REFERENCIAS BIBLIOGRÁFICAS

1.  Cabeza García, P. M. (2021). De la Ley de Benford a la deteccion de fraudes. Revista Universidad y Sociedad, 13(4), 461-467. https://orcid.org/0000-0002-0748-906X

2.  Hassler, U., & Hosseinkouchack, M. (2019). Testing the Newcomb-Benford Law: experimental evidence. Applied Economics Letters, 26(21), 1762–1769. https://doi.org/10.1080/13504851.2019.1597248

3.  Gorenc, M. (2019). Benford’s Law As a Useful Tool to Determine Fraud in Financial Statements. Management, 14(1), 19–31. https://doi.org/10.26493/1854-4231.14.19-31

4.  Handoko, B. L., Willy, & Ricky. (2022). Application of Benford Law in Preventing Accounting Data Fraud. ACM International Conference Proceeding Series, 46–51. https://doi.org/10.1145/3535782.3535789

5.  Kössler, W., Lenz, H. J., & Wang, X. D. (2019). Is the Benford Law Useful for Data Quality Assessment. 13th International Workshop on Intelligent Statistical Quality Control 2019, IWISQC 2019 - Proceedings, 391–406. https://doi.org/10.1007/978-3-030-67856-2_22

6.  Morales, H. R., Porporato, M., & Epelbaum, N. (2022). Benford’s law for integrity tests of high-volume databases: a case study of internal audit in a state-owned enterprise. Journal of Economics, Finance and Administrative Science, 27(53), 154–174. https://doi.org/10.1108/JEFAS-07-2021-0113

7.  Barabesi, L., Cerasa, A., Cerioli, A., & Perrotta, D. (2018). Goodness-of-Fit Testing for the Newcomb-Benford Law With Application to the Detection of Customs Fraud. Journal of Business and Economic Statistics, 36(2), 346–358. https://doi.org/10.1080/07350015.2016.1172014

8.  Qu, H., Steinberg, R., & Burger, R. (2020). Abiding by the Law? Using Benford’s Law to Examine the Accuracy of Nonprofit Financial Reports. Nonprofit and Voluntary Sector Quarterly, 49(3), 548–570. https://doi.org/10.1177/0899764019881510

9.  El Mouaaouy, F., & Riepe, J. (2018). Benford and the Internal Capital Market: A Useful Indicator of Managerial Engagement. German Economic Review, 19(3), 309–329. https://doi.org/10.1111/GEER.12129

10.  Tošic, A., & Vicic, J. (2021). Use of Benford’s law on academic publishing networks. Journal of Informetrics, 15(3), 101163. https://doi.org/10.1016/j.joi.2021.101163

11.  Moreno-Montoya, J. (2020). Benford´s Law with small sample sizes: A new exact test useful in health sciences during epidemics. Salud UIS, 52(2). https://doi.org/10.18273/REVSAL.V52N2-2020010

12.  Ceola, S., & Domeneghetti, A. (2023). Potential applications of the Benford&amp;#8217;s Law for the investigation of hydrological time series alteration. https://doi.org/10.5194/EGUSPHERE-EGU23-11797

13.  Singh, N., & Bansal, R. (2015). Analysis of Benford’s law in digital image forensics. 2015 International Conference on Signal Processing and Communication, ICSC 2015, 413–418. https://doi.org/10.1109/ICSPCom.2015.7150688

14.  Parnak, A., Baleghi, Y., & Kazemitabar, J. (2022). A Novel Image Splicing Detection Algorithm Based on Generalized and Traditional Benford’s Law. International Journal of Engineering, Transactions A: Basics, 35(4), 626–634. https://doi.org/10.5829/IJE.2022.35.04A.02

15.  Frick, R. A., Liu, H., & Steinebach, M. (2020). Detecting double compression and splicing using benfords first digit law. ACM International Conference Proceeding Series. https://doi.org/10.1145/3407023.3409200

16.  Lascano Corrales, E. E., & Vega Quiroga, G. (2021). Relación de la ley de Benford con resultados en elecciones seccionales de la alcaldía del Distrito Metropolitano de Quito en 2019. Uniandes EPISTEME, 8(4), 594-593., 8(1390–9150). ISSN 1390-9150

17.  Gueron, E., & Pellegrini, J. (2022). Application of Benford–Newcomb law with base change to electoral fraud detection. Physica A: Statistical Mechanics and Its Applications, 607. https://doi.org/10.1016/J.PHYSA.2022.128208

18.  Eichhorn, K. (2022). Digitalización del menú de manipulación: análisis forense electoral de las elecciones para gobernador de Rusia. Demokratizatsiya: Revista de Democratización Postsoviética, 3, pág. 283-304. https://doi.org/muse.jhu.edu/article/860669

19.  Álvarez Gómez ME, Méndez Cabrita M, Coka Flores DF, Rodríguez Reyes CG. Neutrosociology for Analyzing Public Procurement in Ecuador around the Health Emergency. Neutrosophic Sets and Systems. 2021;44(1). Disponible en: https://digitalrepository.unm.edu/nss_journal/vol44/iss1/37

20.  González Chico, M. G., Hernández Bandera, N., Herrera Lazo, S., & Laica Sailema, N. (2021). Assessment of the relevance of intercultural medical care. Neutrosophic sampling. Neutrosophic Sets and Systems, 44(1). Recuperado de https://digitalrepository.unm.edu/nss_journal/vol44/iss1/46

21.  Guallpa Zatán LG, Paillacho Chicaiza HJ, Yaguar Mariño J, Aguilar Carrión M. Neutrosophic Iadov for measuring user satisfaction in a virtual learning environment at UNIANDES Puyo. Neutrosophic Sets and Systems. 2020;34(1). Disponible en: https://digitalrepository.unm.edu/nss_journal/vol34/iss1/16

FINANCIACIÓN

Ninguna.

CONFLICTO DE INTERÉS

Los autores declaran que no existe conflicto de intereses.

CONTRIBUCIÓN DE AUTORÍA

Conceptualización: Mayra Alexandra Granda Sanmartín, Edgar Ernesto Lascano Corrales, Carlos Iván Lucina Cabezas, Pedro Homero Janeta Tenelema.

Curación de datos: Mayra Alexandra Granda Sanmartín, Edgar Ernesto Lascano Corrales, Carlos Iván Lucina Cabezas, Pedro Homero Janeta Tenelema.

Análisis formal: Mayra Alexandra Granda Sanmartín, Edgar Ernesto Lascano Corrales, Carlos Iván Lucina Cabezas, Pedro Homero Janeta Tenelema.

Investigación: Mayra Alexandra Granda Sanmartín, Edgar Ernesto Lascano Corrales, Carlos Iván Lucina Cabezas, Pedro Homero Janeta Tenelema.

Metodología: Mayra Alexandra Granda Sanmartín, Edgar Ernesto Lascano Corrales, Carlos Iván Lucina Cabezas, Pedro Homero Janeta Tenelema.

Administración del proyecto: Mayra Alexandra Granda Sanmartín, Edgar Ernesto Lascano Corrales, Carlos Iván Lucina Cabezas, Pedro Homero Janeta Tenelema.

Recursos: Mayra Alexandra Granda Sanmartín, Edgar Ernesto Lascano Corrales, Carlos Iván Lucina Cabezas, Pedro Homero Janeta Tenelema.

Software: Mayra Alexandra Granda Sanmartín, Edgar Ernesto Lascano Corrales, Carlos Iván Lucina Cabezas, Pedro Homero Janeta Tenelema.

Supervisión: Mayra Alexandra Granda Sanmartín, Edgar Ernesto Lascano Corrales, Carlos Iván Lucina Cabezas, Pedro Homero Janeta Tenelema.

Validación: Mayra Alexandra Granda Sanmartín, Edgar Ernesto Lascano Corrales, Carlos Iván Lucina Cabezas, Pedro Homero Janeta Tenelema.

Visualización: Mayra Alexandra Granda Sanmartín, Edgar Ernesto Lascano Corrales, Carlos Iván Lucina Cabezas, Pedro Homero Janeta Tenelema.

Redacción – borrador original: Mayra Alexandra Granda Sanmartín, Edgar Ernesto Lascano Corrales, Carlos Iván Lucina Cabezas, Pedro Homero Janeta Tenelema.

Redacción – revisión y edición: Mayra Alexandra Granda Sanmartín, Edgar Ernesto Lascano Corrales, Carlos Iván Lucina Cabezas, Pedro Homero Janeta Tenelema.